Building a Sound Macroscopic Theory of Matter and Deeper Epistemological Understandings of Science Among Elementary & Middle School Students
Carol L. Smith
University of Massachusetts at Boston
My colleagues and I have been investigating what it takes to help middle school students build a sound macroscopic theory of matter in which the concepts of mass, volume, and density are clearly distinguished and inter-related. We have also been investigating the classroom conditions that may foster elementary school students' greater understanding of how knowledge is created and justified in science.
Within each area, our research has had a two-pronged focus. First, we have tried to provide rich descriptions of students' starting conceptions and the ways they may be organized in commonsense theories that are at odds with the theories that students will be expected to learn at school. One of the things that makes the science curriculum so challenging is that it needs to help students engage in a process of fundamental conceptual change or restructuring, not simple conceptual elaboration. Understanding the nature and organization of student initial ideas is an important first step to planning effective science curricula that will promote conceptual change.
Second, we have carried out numerous teaching studies that compare the effectiveness of different curricular approaches in bringing about conceptual change. In this way, we have been trying to understand the underlying mechanisms of conceptual change (e.g., the role of processes such as analogical mapping, model building, and thought experiments) and the classroom conditions that may support such changes.
Because I do not have time now to prepare a special paper for this conference, I have chosen to share excerpts from two previously published papers. For each article, I have included (a) the abstract, (b) excerpts that describe the target conceptions to be taught, the organization of student initial conceptions and the conceptual changes that need to be made in the given area, and (c) excerpts that describe some of my thinking on what it takes to enable students to make these conceptual changes.
I. Building a Sound Macroscopic Theory of Matter in the Middle School Years
Excerpts from:
Smith, C., Maclin, D., Grosslight, L., & Davis, H. (1997) Teaching for
Understanding: A Study of Students' Preinstruction Theories of Matter and
a Comparison of the Effectiveness of Two Approaches to Teaching about Matter
and Density". Cognition and Instruction, 15(3), 317-393. Copyright ©
1997, Lawrence Erlbaum Associates, Inc.
A. Abstract (pp. 317-318): Thirty 8th-grade students were given an interview and a written test before and after a 10-week curriculum unit concerning matter, mass, volume, and density. The instruments probed qualitative understandings of matter; ability to differentiate weight and density using qualitative reasoning; formal quantitative understandings of mass, weight, volume, and density; and ability to integrate both qualitative and quantitative reasoning about density. In part 1 of the study, we examined the organization of student ideas prior to instruction. We found evidence to support our idea that students' qualitative conceptions of matter and density were organized in commonsense theories of matter that constrained their understanding of density: Students who believed that all material objects have weight, no matter how small or light the object, were much more likely to have made a beginning differentiation between weight and density than those who did not. We also showed that a qualitative understanding of density emerged prior to a formal, quantitative understanding of density, although most students were able to engage in explicit proportional reasoning about another, more familiar quantity (i.e., sweetness). In Part 2, we compared the effectiveness of two teaching approaches. One approach to teaching about matter and density—the standard Introductory Physical Sciences (IPS) curriculum—emphasized formal definitions, measurement, and explicit quantitative reasoning. Because it asked students to work formally with complex concepts before assuring the relevant qualitative understanding was in place, we designed a modified IPS curriculum that addressed this problem by encouraging students to make their initial assumptions about matter explicit and open to debate. The modified curriculum also used visual models and qualitative reasoning to help students bridge the gap between their starting conceptions and formal, quantitative definitions. We found that both curricula were effective in promoting a good quantitative understanding of mass, volume, and density. The modified curriculum, however, was more effective at restructuring students' qualitative conceptions and at promoting an integrated understanding of density. Thus, we conclude that science curricula should integrate both qualitative and quantitative reasoning to be effective at promoting conceptual change.
B. Excerpt from the Introduction that describes some important aspects of the target conceptions to be taught (pp.318-320):
There is increasing interest in the science education community in "teaching for understanding" (Clement, in press; Perkins, Schwartz, West, & Wiske, 1995). But what is involved in scientific understanding? How can it be developed?
Clement (in press) argued that three important hallmarks of scientific understanding are the abilities to: (a) decide when it is appropriate to apply a scientific principle, (b) solve problems quickly on the basis of insightful, often qualitative reasoning, and (c) transfer knowledge flexibly to new situations. To study the reasoning processes experts use for understanding new situations, he asked expert scientists to think aloud as they reasoned about challenging, novel problems. His analyses revealed an extensive "hidden world" of non-formal reasoning processes used by experts. These processes included analogical reasoning, mental model construction, spatial reasoning using dynamic visual imagery, reasoning using kinesthetic intuitions and hand motions, and reasoning based on consideration of extreme cases or imagined thought experiments (gedankenexperiments). Clement (1989, in press) argued these non-formal processes help experts figure out which principles apply in new situations and generally ground, or give meaning to, more abstract mathematical formulations of ideas and theories. Similarly, Nercessian (1993) described the rich and productive interplay between nonformal imagistic reasoning and more formalized mathematical reasoning in her historical case study of the development of Maxwell's ideas about electromagnetism.
Clement's (1989, in press) and Nercessian's (1993) rich analyses of expert competence have important implications for approaches to science instruction. If experts flexibly apply both formal and non-formal reasoning strategies to develop good understandings of novel problems, it follows that good science instruction should help students to develop skill at both kinds of reasoning. Yet, traditional approaches to science instruction at the middle school level or later typically aim to help students to develop only the more formal kinds of reasoning. The bulk of this kind of curriculum content and teaching consists of explicit and formal definitions for concepts, equations, formulas, and practice in how to apply these formulas in certain stereotyped problem situations. Students are seldom encouraged to reason qualitatively about conceptual relations starting from their own commonsense ideas, to construct qualitative models of phenomena, or to refine their own intuitions about the physical world.
This study first examined the extent to which students entered the classroom with qualitative, physical intuitions about matter, weight, and density that were at odds with the formal concepts that comprise their science curriculum. It also examined the extent to which these intuitions were organized in commonsense theories of matter. It then explored the impact of two forms of instruction on the development of student concepts of matter and on their ability to differentiate the concepts of weight and density. Scientific concepts like density have important formal and non-formal components. We believe that a robust understanding of density calls for the integration of these formal and nonformal components and that effective science teaching needs to provide opportunities for the practice and integration of both forms of understanding.
Formally, density is defined in the middle school science curriculum as a ratio quantity (the mass to volume ratio) or as a per quantity (the mass per unit volume) that is a characteristic property of different materials (i.e., a property that can be used to distinguish one material from another). This characteristic property cannot be directly perceived, but can be determined by calculation by first explicitly measuring the mass and volume of a given object and then dividing the mass by the volume.
Nonformally, the concept of density is grounded in qualitative physical intuitions developed from interaction with everyday materials. For example, solid objects can be the same size but different weights (e.g., a block of wood and a block of steel) and very small objects can be much heavier than larger ones. If one notices that these objects are made of different kinds of materials, one can infer that some objects are made of "heavier kinds of materials" than others. A number of qualitative rules then allow one to make inferences about this characteristic of materials; for example: (a) If two objects have the same size but different weights, the heavier object is made of a heavier kind of material; (b) if two objects have the same weight but different sizes, the smaller object is made of a heavier kind of material; and (c) if two objects are made of the same material, they have the same density because equal-sized pieces would have the same weight. Finally, one can use everyday experiences with packing (i.e., with how close together or far apart items are) to begin to explain this characteristic of materials (e.g., by imaging that objects vary in how much material is packed into a given space).
We believe that good science education needs to recognize the existence and importance of both formal and informal sources of understanding and to encourage students to develop supporting physical intuitions for more formal concepts. Clearly, an intuitive concept of density is, by itself, limited. Mathematical tools allow for quantifying the mass and volume of objects and for assigning a numeric value to the density differences of materials. In this way, they extend the range and precision of inferences that can be made about this physical magnitude. Furthermore, this greater precision can be used for discovering new patterns in data and for engaging in the iterative process of generating, testing, revising and transforming models. It is possible, for example, to move beyond an initial qualitative model of density based solely on the idea of differential packing of homogeneous matter to a model that builds on atomistic frameworks. Such models can be used to explore the relative importance of packing versus differing atomic weights as explanations of density differences among materials.
A formal concept of density, however, unsupported by physical intuition, qualitative reasoning, and visual models is also limited. Non-formal notions guide students in making appropriate inferences in those situations where precise measurement is not possible, give them a quick way of checking the reasonableness of more formal calculations, and as Clement (1989, in press) argued support scientific inventiveness by permiting the building and testing of rough qualitative models of new phenomena and situations.
C. Excerpt that describes student initial conceptions as organized in a commonsense matter theory (Commonsense Matter Theory 1) and contrasts this theory with a more sophisticated commonsense theory that some students have developed (Commonsense Matter Theory 2). The latter view is closer to the target macroscopic theory of matter that is taught in middle school (pp. 322-324):
Commonsense Matter Theory 1 has its own coherence and integrity, with students' conceptions of matter supporting their combination of the properties of heavy and heavy-for size into one undifferentiated weight-density concept (also known as conflating weight and density into one concept). In this theory, students define matter as something readily observable that can be touched, seen, and felt. They believe material bodies are impenetrable (in the sense that two bodies cannot occupy the same space at the same time) and believe that material bodies can causally interact with each other. Solids are the prototypical material objects, whereas air is a prototypical nonmaterial object. Students may be less certain about liquids and powders because, although they can be touched and seen, they seem more penetrable. Given that students expect matter to be readily observable, they think that matter ceases to exist when it is too small to see or touch, and they cannot think of material objects as fundamentally continuous (i.e., constituted of matter at every point). Because students do not think of matter as fundamentally continuous, they cannot believe that small pieces of matter have weight; so, they cannot conceive of weight as an additive property of material objects. Weight is felt-weight: an accidental property of some, but not of all material objects; it is a property that emerges when you have enough of the material for something to feel heavy. In making judgments of how heavy something feels, children may employ different standards that are relative to what is most salient in the situation (i.e., heavy-for-me, heavy-for-size) and thus conflate elements of weight and density in one concept. In fact, how heavy something feels is a function of a variety of physical and psychological factors: the overall weight of the object, the pressure on one's hand, weight-size illusions, and the way the object is held with muscles tensed in anticipation.
In contrast, Commonsense Matter Theory 2 supports the differentiation of weight and density. In this theory, students conceive of matter as fundamentally continuous and define matter more abstractly as having weight and volume. Students can now imagine that material objects can be divided into arbitrarily small units, each of which has a definite volume and weight. These small units also preserve material kind and properties special to that kind (e.g., odor, taste, capacity to rot or rust, density). This allows for the possibility that, although neither palpable nor visible, bits of matter maintain their integrity. It also permits students to construct a decompositional analysis of the weight of objects. In such an analysis, the weight of an object is a joint function of the density of the material and the volume of the object. Hence, the core idea in the concept of weight is not felt-weight but a fundamental additive property of matter.
Furthermore, with such conceptions in place, students are now enabled to make a principled distinction between weight and density: They can conceive of density as an intensive property of material kinds that is preserved in decomposition, and they can conceive of weight as an extensive property of matter that reflects the additive sum of the weight of all the component parts. Finally, this new theory provides students with the resources for reexamining their assumptions about the immaterial status of air. To conclude that air is matter, however, students need additional knowledge that air has weight and takes up space.
D. Excerpt that describes conditions for promoting conceptual change and the contrasts between two curricular approaches used in this study (pp. 358-369)
General Framework for a Conceptual Change Approach to Teaching
Posner, Strike, Hewson, and Gertzog (1982) argued that four general conditions must be met in order to promote conceptual change: (a) Students need to be dissatisfied with their current conceptions; (b) students need to find a new conception intelligible; (c) students need to find this new conception plausible; and (d) students need to find this new conception fruitful.
Many different techniques can be employed to help students meet each condition, including some of the kinds of non-formal reasoning discussed by Clement (1989, in press). Arousing a student's dissatisfaction involves awakening a student's interest in a phenomenon, fostering awareness of the student's current conceptions, encouraging the student to make a prediction or inference based on a conception (often qualitative in nature), and helping the student to discover that the prediction or inference is not confirmed. These techniques help students not only to be aware of an anomaly, but also to care about the anomaly and to find it bothersome or dissatisfying. Making a new conception intelligible involves the use of visual pictures or diagrams, familiar analogies, or other kinds of concrete examples to help students connect the new idea with ideas they already have or to construct a new model. Making a new conception plausible involves resolving any discrepancies between the implications of the new idea and students' general knowledge and beliefs, through discussion, gedankenexperiments, limiting case analyses, and other techniques. Finally making a new conception fruitful involves helping students see how the new idea is productive in explaining a wide range of phenomena. Posner et al. (1982) argued that students must find the new idea plausible and fruitful as well as intelligible, if they are going to become committed to the new belief and actually replace their old conception with a new one.
Conceptual change curricula require that students be aware of their own ideas. Assessment tasks, such as written tests and one-on-one clinical interviews, provide one way of posing questions and problems that engage and help to externalize student conceptions. Informed by the results of these probes, the teacher can tailor curriculum activities to further engage and externalize these conceptions in the classroom. Brooks and Brooks (1993) recently discussed classroom techniques teachers can use to uncover, value, and support these beliefs. For example, the teacher can acknowledge that multiple perspectives exist rather than emphasizing that student ideas are right or wrong, provide opportunities for students to express their point of view and to communicate with each other, pose questions and problems to students that are helpful in drawing out current student conceptions, listen carefully and respectfully to students' ideas and ask them to elaborate or explain their ideas further, and give students opportunities to reflect on their ideas (e.g. by asking students to reexamine their past work as their ideas evolve).
These teaching techniques also call on students to take an active cognitive, emotional and social roles in the process of restructuring their concepts and building new ideas. They, like their teachers, must acknowledge "that one's own view is not the only one nor necessarily the correct one, but is one of many" (Brooks and Brooks,1993, p. 58). They must be willing to articulate their point of view, to wait and listen while peers express ideas, to dialogue about beliefs with peers, to think deeply about questions and problems, to elaborate on and justify their responses, and to reflect on their conceptions. Indeed, achieving conceptual change may depend on students' success in engaging in these important processes (White & Gunstone, 1989)
Hennessey & Beeth (1993) recently proposed that upper elementary students are capable of learning the meta-language of conceptual change theory (e.g., dissatisfaction, intelligibility, plausibility, fruitfulness), and that using this language in the classroom facilitates the kinds of class discussion that are important in conceptual change teaching. Such vocabulary aids students in taking the responsibility for monitoring the intelligibility and plausibility of ideas. It also can provide valuable feedback to teachers about the progress of the lessons because students' comments during class directly reveal to the teacher where students are in accepting an idea.
With this brief review of the conceptual change literature as a backdrop, we now turn to describing the two curricular approaches being contrasted in the present study and examine how well the two curricula meet the many conditions for conceptual change.
Overview of the Two Curricula
Curriculum developers in the 1960's developed IPS in response to traditional, textbook-based science curricula that tried to teach students the content of science without involving them in the process of science. They intended IPS to teach students about matter and science "inductively," by involving them in conducting, writing about, and discussing many firsthand experiments. Because these curriculum developers were not as attuned to the specific qualitative conceptions students brought with them to science class, the IPS curriculum was not explicitly organized around helping students articulate and test their conceptions against new alternatives. Rather it was based on an assumption that students would converge on certain scientific ideas and laws by simply performing and discussing a series of experiments.
The focus of this study is on the conceptual changes brought about during one part of the IPS curriculum (chapter 2 and 3). IPS shares our assumption that prior to developing an understanding of the particulate nature of matter, students need to develop an appropriate macroscopic theory of matter. Chapters 2 and 3 in the IPS textbook aim to articulate a macroscopic theory of matter in which the quantities of mass, density, volume are all clearly distinguished and inter-related. Matter is defined in terms of having mass and volume: Solids, liquids and gases are all phases of matter. Mass is considered the best measure of the amount of matter in an object because it is the mass, not the volume of objects, which is conserved across various physical transformations such as dissolving and heating. Density is defined as mass per unit volume, with different material kinds having different characteristic properties (e.g., different densities, boiling points and freezing points).
We designed our modified IPS curriculum to build on the strengths of the IPS approach, following the main logic of chapters 2 and 3 and covering many of the same experiments. We believed, however, that the developers of IPS made incorrect assumptions about how well students understand concepts that are fundamental to achieving a robust understanding of density; we also believed that they underestimated the number of conceptual hurdles students face in coming to understand these concepts, and the importance of engaging students in qualitative reasoning to bridge between initial commonsense intuitions and more formal concepts. We designed the modified curriculum to meet the conditions of conceptual change described by Posner et al. (1982). We incorporated many of the strategies noted earlier from the conceptual change literature in order to make fundamental concepts explicit and visible, to help students become aware of and explore their commonsense intuitions, and to gain the qualitative understanding necessary for comprehending the formal concept of density. We did not attempt, however, to teach students a meta-language for monitoring changes in the status of their conceptions as did Hennessey and Beeth (1993). In the sections that follow, we describe the contrasting approaches taken to teaching students about the properties of matter (chapter 2) and about density as a characteristic property of material kinds (chapter 3).
The Properties of Matter: The Standard IPS Curriculum
From the very first paragraph and throughout chapter 2, the IPS text assumes that the following points are unproblematic: Students have a conception of matter that includes gases, they readily accept that all matter has mass and volume, and students understand that very small objects have mass and that the mass of the whole object is a function of the mass of its parts. Students encounter experiments that are based on these assumptions; yet, the experiments are not performed for the explicit purpose of testing these points. In one experiment, for example, students are asked to estimate the mass of a gas produced in a chemical reaction as part of testing the law of conservation of mass, not as part of establishing that gases are material and must have mass. Doing the experiment for this reason fails to challenge students to consider how the implications of this experiment bear on their basic conceptions about the non-material nature of air.
In the class with the standard IPS curriculum, students were not asked what they think the defining features of matter are, or what entities they include in the matter category. Thus, students did not articulate their own "commonsense views" of matter (typically that matter is something that can be seen and held, and something which excludes air). Because students did not have to articulate their views, they were not likely to be very aware of them or become dissatisfied with them. No classroom time was devoted to discussing how the commonsense properties of matter (seeing and feeling) compare and contrast with the scientist's properties of matter (taking up space and having mass).
With no acknowledgment that students hold alternative views to the physicist's about what entities are matter or how matter is defined, no attempt was made to show that the physicist's view is more plausible or fruitful than the students' commonsense view. Thus, we believe that these students assumed that their personal views and the scientist's view incorporated the same concepts and that they simply merged the two views together (i.e., adding the beliefs that matter has mass and volume to their initial commonsense beliefs that matter can be touched, seen and held.) For example, students did a complicated Alka-seltzer® experiment in which they measured the total mass of a dry tablet of Alka-seltzer® and a capped bottle of water; the total mass of the Alka-seltzer® dissolved in the capped bottle of water; and the total mass of the dissolved Alka-seltzer® in the capped bottle of water after the bottle has been uncapped and the resulting CO2 gas released). As mentioned earlier, however, the focus of the experiment was on the idea that mass is conserved across chemical transformations and not on establishing the prior point that gases must be material.
In Chapter 2, the fundamental puzzle for students is: "Which is a better measure of the amount of matter: its volume or mass?" Students in the standard IPS curriculum experimented with several situations in which the volume of the matter changes when no matter is added, and the mass remains the same. Then they pursued six more experiments (with solids, liquids, and gases) that showed that, under a variety of dramatically different transformations, mass is always conserved. The unit (and chapter) culminated in the statement of the law of conservation of mass.
To the extent that students start with the belief that volume is a good measure of the amount of matter in an object, we would argue that the standard IPS curriculum should be effective in arousing dissatisfaction with this initial belief and in making intelligible the new view that mass is a better measure of the amount of matter. In addition, it should be effective in showing the fruitfulness of this new view because it accounts for a wide range of phenomena. Its only weakness may be in helping students establish the plausibility of this view. The curriculum does not consider that students might have alternative views about matter (e.g. a continuous conception of matter) which would make it hard to understand how the volume of an object can change while its mass remains the same. It relies on students to accept this phenomenon as an empirical law or observation at this point. Explanatory model building is introduced much later (Chapter 8) to help explain the law of constant proportions. If model building were introduced from the outset as central to the scientific enterprise, students might have a chance to use this powerful tool throughout the curriculum.
The Properties of Matter: The Modified IPS Curriculum
In light of our findings that some students think that air is not matter and that some material objects (such as pieces of Styrofoam) weigh nothing at all, we designed our modified curriculum to address a broader series of questions: How can one distinguish between matter and non-matter? What are the fundamental properties of matter? How can the mass and volume of objects be measured? Do small objects have measurable volume and mass? Which is a better measure of the amount of matter in an object: an object's mass or volume?
We began by initiating a whole class discussion about what is and what is not matter. Is a rock matter? What about sugar, water, air, smoke, light, a shadow, or an idea? Most students agreed that solids and liquids are matter. They engaged in lively debate, however, about whether gases, heat, and light are matter or not matter, and about what the defining properties of matter could be. Our main purpose was to uncover student ideas and reasons for those ideas, and to promote awareness of multiple views and areas of agreement and controversy.
Then, we asked students to investigate the properties of matter in the "clear cases," that is, solids and liquids: Do all solids and liquids have measurable volume and mass? We wanted students to develop an understanding of how volume and mass are measured and to develop skill at making these measurements. Students then examined whether very small or very light objects had volume or mass. For example, students were challenged to find the volume of a piece of paper, the thickness of which seemed initially unmeasurable. Students constructed a variety of ingenious solutions to this problem, including measuring the volume of a ream of paper and then dividing by the number of sheets of paper.
To address the issue of the mass of very light objects, students first massed 50, 10, 5 lentils, and then, they massed 1 single lentil on a balance scale and described the resulting pattern observed in this sequence of mass measurements. They next considered whether half a lentil had any mass, and if so, to devise a way to estimate the mass of half a lentil. This activity led the class to consider using the mathematical operation of division to solve this problem, and to engage in gedankenexperiments about the repeated divisions of a quantity.
Next, in a video of two classmates performing a series of experiments on an analytical balance, students saw that this balance (sensitive to masses of 1/10,000 of a gram) can measure the mass of a variety of light objects (e.g., one fleck of glitter or an inked signature on a piece of paper). They also saw two pennies massed on scales of different sensitivities. The pennies had the same mass on the less sensitive digital scale (sensitive to 1/100 of a gram), but had different masses according to the analytical balance. Thus, students had the chance to observe and discuss the issue of scale sensitivities, and to realize how imprecise and inaccurate their own perceptual judgments can be. We believed these extreme cases considered in this activity helped challenge their conceptions of weight as felt weight and their over-reliance on their own felt-weight perceptions.
Once the students were convinced that all solids and liquids have measurable volume and mass, they were asked: "Which is a better measure of the amount of matter: the volume of an object or its mass?" Then students performed the series of experiments in the IPS curriculum which address this issue with solids and liquids. This portion of the curriculum was largely the same in both classrooms.
Finally, we re-presented the question of whether gases are material and, after reflecting, students suggested doing experiments to see if a gas has volume and mass. After doing several classroom demonstration experiments, the class as a whole performed the IPS Alka-Seltzer® experiment, which showed, among other things, that the mass of the gas is measurable, and helped to confirm that gases must be matter.
Density as a Characteristic Property of Materials: Standard IPS Curriculum.
In Chapter 3 of IPS, students consider three characteristic properties of materials: boiling points, freezing points, and density. Students in the standard curriculum first did the experiments on boiling and freezing points and then moved on to experiments on density. They were introduced to the concept of density by reading aloud from and discussing a portion of Chapter 3 (and then rereading this section for homework). The text asked students to imagine an aluminum rod cut up into sections of equal volume, 1 cm3 each, and note that each section would have the same mass regardless of the part of the rod from which it came. The text then notes that the mass of 1 cm3 of water is different from the mass of 1 cm3 of aluminum. Therefore, the text concludes, the mass of a volume unit is a characteristic property of a material that can be used to distinguish different materials.
The next paragraph discusses that it is rare to directly measure the mass of 1 cm3 of a substance. Instead, scientists usually find the total volume and total mass of an object, and calculate the mass of a unit of volume by dividing the total mass by the total volume, which results in the density of the material.
In these two paragraphs, the book presents the formal concept of density to students. Neither the book nor the teacher presented students with any explicit pictures or models. Without such pictures, students who enter with an undifferentiated weight/density concept might find it hard to distinguish between the mass of the entire object and the mass of a unit of volume and, hence, might find the book definition unintelligible. The teacher did supplement the formal book definition by saying that denser materials were somehow "more tightly packed," although he was careful not to discuss atoms or molecules at this point, because he did not want to introduce any scientific jargon that was not carefully motivated by the students' experimental findings. In IPS, experimental findings concerning the law of constant proportions in chemical reactions are introduced at the end of the curriculum (chapter 8) to motivate an atomistic conception of matter.
Students went on to do the labs, which involve finding the densities of various solids, liquids, and gases. The lab for finding the density of a gas involved a very elaborate procedure that took several days to complete. Throughout this lab, students made quantitative measurements of mass and volume to calculate density, used density differences to help them decide whether objects are made of the same or different substances, considered the nature of experimental error, and also compared the range of densities found in solids, liquids, and gases. Finally, they worked through all the word problems posed at the end of each lab. Many of these problems gave students explicit data about the mass and volume of some matter and asked them to infer its density or whether the entities in question are made of the same substance. They were also given practice in carrying out algebraic procedures for solving "missing value problems". Using the formula for density (Density = Mass/Volume), they substituted x for the unknown quantity, and solved for it.
Students never engaged, however, with qualitative puzzles that would challenge their undifferentiated concept of weight/density. For example, how can a large heavy piece of aluminum (e.g., 500 gm) have the same density as a small light piece of aluminum (e.g., 1 gm)? Or, how can a large heavy piece of wood be less dense than a small light piece of brass? Thus, they were neither made aware of their initial views about density nor introduced to how the scientist's view would be more plausible and fruitful than their own. Rather, students were given a mathematical procedure for determining density and were given practice with applying that formula to data gathered for solids, liquids, and gases. Whether students deeply understood that procedure depended on how well they understood the original IPS explanation for density. We would expect that only those students who already subscribed to a decompositional analysis of weight had a chance to understand the IPS explanation when it was presented to them.
Near the conclusion of the chapter, the teacher brought in a hydrometer and students worked through a word problem in which they consider how a hydrometer is used to measure the densities of various unknown liquids. This problem presupposed that students' understood that density is relevant to the phenomenon of sinking/floating; however, no explicit experiments were done to develop this understanding.
Finally, students read the portion of the text that describes how the density of a substance changes with heating, although they did no firsthand experiments with thermal expansion. The question in the book is, "Is the density of a substance always the same?" The answer in the book is the following:
Most substances expand when heated but their mass remains the same. Therefore, the density depends on the temperature, becoming less as the material expands and increases in volume .... The expansion is very small for solids and liquids and has little effect on the density. The situation is quite different with gases, which show a large thermal expansion." (Haber-Schaim et al., 1987, p. 62)
Although this portion of text acknowledges that materials do change density with heating, the bulk of chapter 3 is devoted to making the point that density is a characteristic property of materials and does not challenge students' emerging notion that the density of materials remains constant..
Density as a Characteristic Property of Materials: Modified IPS Curriculum
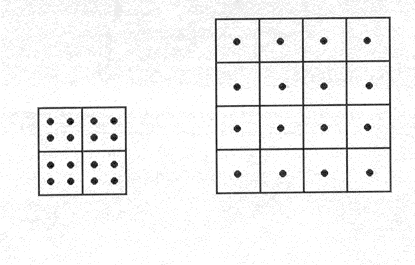
The use of conceptual models to introduce the concept of density is central to the rationale of the modified IPS curriculum. This rationale has been described extensively elsewhere (e.g., Snir, Smith, and Grosslight, 1993). Briefly, the idea behind a conceptual model is to give students a way of visually representing concepts, which are not seeable or initially differentiated, by exploiting immediately apprehensible and differentiated visual analogs which have the same relational structure as the abstract physical concepts. The conceptual model gives students a way of concretely representing a conceptual distinction that is not representable in terms of their current matter framework and provides them with guidance about how their framework needs to be restructured. Figure 3 shows one of the conceptual models we used in the modified IPS curriculum. One elegant advantage of this model is that volume, mass, and density are portrayed using three distinct, yet inter-dependent visual referents. Thus, the visual model embodies the assumptions of a decompositional matter theory and the quantitative relations in the mathematical formula for density.
|
Figure 3. An example of a conceptual model used in the modified Introductory Physical Science curriculum. In this model, a box represents a volume unit, a dot represents a mass unit, and the number of dots per box represents the density of the material. |
We began the unit by presenting a multistep problem about the feeding behavior of different fish. The problem involved several different per quantities. Students were directed to draw models which accurately portrayed the information in the "givens" in order to clarify their ideas and devise solutions. Thus, students experienced how model building was a useful tool to help integrate information, clarify ideas, and solve problems. While discussing and comparing their different models, students also had the opportunity to talk explicitly about some metaconceptual notions about models. These points included that there can be more than one way to model the same problem, that a good model should be faithful to the known facts and should use codes in a consistent way, that models can vary in terms of how picture-like they are, and that it is often not important for the model to look like what it is modeling, as long as it conveys information about key relationships (in this case, the key per relationships).
Students then created pencil and paper models for population density and sweetness, and worked with our computer-based dots-per-box models for these same phenomena. The purpose of these activities was to give students further experience in creating and working with models of per quantities and to make sure they clearly differentiated between "total number of dots" and "dots per box" in our models.
In introducing the concept of density of materials, we presented a puzzle. Students were asked the following about three different-sized objects of different materials that were painted the same color: Could these objects be made of the same material? How can you tell? What do you think the distinguishing properties of different materials are? These were the same three objects used in the standard IPS lab on finding the density of solids. However, in the standard lab, students are given the procedure for finding density (i.e., D=M/V) and were simply asked to apply it to finding the density of the objects.
In reasoning about this puzzle, students in the modified IPS curriculum mentioned that they thought that some objects were made of heavier kinds of materials than others. The teacher then asked them to create models to help clarify their ideas. Same-sized cubes of aluminum and brass (27 cm3) were then brought out and measured, and students were encouraged to draw a model which connected their data about mass and volume and showed how the mass is distributed in each object. In their models, students generally used one large box to depict the entire 27-cm3 cube, which they filled with different numbers of dots. They also developed a key to indicate how many grams a given dot stood for. The teacher asked: Does your model give you any clues about what might be a distinguishing or characteristic property of materials? Students then discussed and compared their models as a lead-in to working with the "mass icons per box" model, the kingpin of the computer software we designed to help students construct an understanding of mass, volume, and density (Snir et al., 1993). At this point the word density was introduced and defined vis-a-vis these models as mass per unit volume.
Students spent about three lessons working with a series of computer-based conceptual models and simulations that we had designed to help them distinguish mass (or weight) and density, and to explore the related real-world phenomenon of flotation. We believe that using computer software had manifold advantages. In particular, our computer software allows different representations to be presented simultaneously (e.g., pictorial, conceptual, data table, graphic). These linked representations provide a means of enriching understanding of less familiar representations by working with more meaningful representations. They also provide visual representations for unseen conceptual relations, and allow students to perform experiments using these conceptually enhanced representations as a tool for guiding discovery. Our computer simulations allow students to do informative experiments easily that would be much harder to do in the real world. For example, students find it extremely difficult to measure the mass and volume of different samples of the same kind of material with enough accuracy to determine that different sample sizes do, in fact, have the same density. Doing simulations on the computer, however, allows them to see that increasing the volume proportionately increases the mass, explaining why the density must remain a constant. Such an ideal simulation prepares students for dealing with the experimental error that occurs in the lab. Finally, our software offers students personal control over the nature of the representations used and the time spent reflecting on a phenomenon of interest or difficulty.
Students used these computer simulations to enhance their understanding and reflection about real-world phenomena and not as a substitute for doing lab experiments. For example, working with these simulations helped students to see what happens to an object's mass and density when its size was increased and how varying material kind for equal-sized objects affected the object's mass and density. Once such an understanding was firmly in place, students returned to the lab to see if they could verify that different-sized objects of the same material have the same density. In this context, students were more prepared to interpret observed variations as experimental error rather than true density differences because they had the firm expectation that the mass and volume relation should be the same for all sample sizes of the same material.
To establish the fruitfulness of the concept of density, students also briefly investigated two other phenomena where the concept of density was useful: (a) sinking and floating and (b) thermal expansion. First, they investigated sinking and floating of real objects in the lab. They used qualitative observations of an object's material kind, relative mass, and relative volume to predict how it would behave in water, test their predictions, and make up a general rule to predict sinking or floating of any object in water. Students then continued their explorations of sinking and floating by using computer simulations. These simulations allowed them to test more easily the effects of different variables on sinking and floating (e.g., mass, volume, density of material) and to experiment with liquids of different densities. This allowed them to formulate a rule for sinking and floating that focused on the relation between the density of the object and the density of the liquid, rather than simply on the density of the object.
Finally, students explored the phenomenon of thermal expansion, using a "ball and ring" demonstration (a heated ball does not pass through a ring) and an "expanding oil" demonstration. In both cases, students saw that the volume increased and the mass stayed the same. (For the ball and ring, the observations about mass and volume were qualitative, whereas for oil quantitative data was presented). Students modeled the situation for themselves so they could work out what happened to the density of the brass ball and oil. These models helped students to see that although density is a characteristic property of materials (at a given temperature), the density of a material changes with heating. Finally, students were invited to reflect on whether or not heat was matter, given that we found that a heated and unheated ball had the same mass.
II. Developing Students' Epistemological Ideas about Science
Excerpts from:
Smith, C., Maclin, D., Houghton, C. and Hennessey, M. (2000) Sixth-Grade Students'
Epistemologies of Science: The Impact of School Science Experiences on Epistemological
Development. Cognition and Instruction, 18(3), 349-422. Copyright © 2000,
Lawrence Erlbaum Associates, Inc.
A. Abstract (p. 349): Previous studies have documented that middle school students have a limited "knowledge unproblematic" epistemology of science (i.e., scientists steadily amass more facts about the world by doing experiments) with no appreciation of the role played by scientists' ideas in guiding inquiry. An important question concerns to what extent students this age and younger are ready to restructure their epistemological views to focus on more "constructivist" issues: the conjectural, explanatory, testable, and revisable nature of theories. This study tests the claim that even elementary school students can make significant progress in developing a more sophisticated, constructivist epistemology of science, given a sustained elementary school science curriculum that is designed to support students' thinking about epistemological issues. To assess the impact of elementary science experiences on students' epistemological views, 2 demographically similar groups of 6th-grade students were individually interviewed using the Nature of Science Interview developed by Carey and colleagues (Carey, 1991; Carey, Evans, Honda, Jay, & Unger, 1989). Both groups had experienced sustained elementary science instruction: 1 taught from a constructivist perspective and 1 taught from a more traditional perspective. We found that students in the more traditional science classroom had developed a "knowledge unproblematic" epistemology of the type previously reported by Carey et al. (1989). In contrast, students in the constructivist classroom had developed an epistemological stance toward science that focused on the central role of ideas in the knowledge acquisition process and on the kinds of mental, social and experimental work involved in understanding, developing, testing and revising these ideas. We conclude that elementary schoolchildren are more ready to formulate sophisticated epistemological views than many have thought. We discuss how these findings relate to the broader epistemological literature, and the features of the constructivist classroom environment that may have supported the development of these sophisticated understandings.
B. Excerpt that contrasts three qualitatively different epistemologies of science (note: elementary and middle school students who have experienced traditional science instruction typically hold Level 1 views) (pp. 356-358)
Carey and Smith (1993) distinguished three qualitatively different epistemologies of science each of which involves a set of different concepts for describing both the structure of scientific knowledge and the processes of knowledge acquisition in science. Movement from one epistemology to another thus involves making fundamental conceptual changes.
At Level 1, scientific knowledge is assumed to consist of a collection of true beliefs about concrete procedures (e.g., how to do something correctly) or basic facts (e.g., what happens). Hence, students at this level make no clear distinction between scientists' ideas and activities or between their ideas and experimental results. They view scientific knowledge as accumulating in piecemeal fashion through simple telling or first-hand observation. They also view it as certain and true. Because they view scientific knowledge as about what to do and what happens, they view experiments as providing certain information about what happens or whether one's procedure works.
At Level 2, scientific knowledge is assumed to consist of a collection of tested ideas. The two new notions that emerge at this level are notions of explanation and hypothesis testing. Students at this level view scientists as concerned with understanding how things work or why things happen. They also view scientists as doing experiments in order to test their ideas to see if they are right and as abandoning or revising their ideas when they find out they are wrong. Both notions of explanation and hypothesis testing require that students make a differentiation among scientists' ideas, activities and experimental results (e.g. the purpose of an experiment is to test a scientist's idea; the purpose of an explanation is to account for an experimental result). Although students appreciate that prior knowledge influences the hypothesis-testing process, they still think absolute knowledge is obtainable with enough diligence and effort. They make no distinction between scientists' overarching theories and specific hypotheses.
At Level 3, scientific knowledge is believed to consist of well-tested theories about the world, which are useful in explaining events and in predicting the outcomes of new events. A theory is understood as a coherent, explanatory framework that consists of a network of hypothetical theoretical entities that are used to explain patterns of data. Students at this level make an explicit distinction between the scientist's guiding theories and more specific hypotheses. They view theories as guiding all aspects of inquiry: the generation of hypotheses, the selection of methods and the interpretation of data. They understand experimental results not only as providing evidence for and against hypotheses, but also as providing support (more indirectly) for and against theories. They also understand that theories, although revisable in principle, are resistant to change and slow to evolve. Ultimately, they judge canons of justification as framework relative and theories as more or less useful rather than strictly right or wrong. Thus, although students at Level 3 view scientific theories as providing rigorous standards for knowing and understanding, they also understand that knowledge of reality is fundamentally elusive and uncertain.
Carey and Smith (1993) note that Level 1 ideas are consistent with what they have dubbed a knowledge unproblematic epistemology (i.e., an epistemology in which knowledge is regarded as true and certain) whereas Level 3 ideas clearly reflect a knowledge problematic epistemology (i.e., an epistemology in which one understands the tentative, framework-relative nature of knowledge). These two contrasting epistemologies are very similar to the starting (absolutist) and ending (constructivist) epistemologies described in the general epistemological literature, although a Level 3 epistemology includes specific reference to the conjectural nature of explanatory theories and the role of indirect argument, evidence, and cycles of hypothesis testing in their evaluation.
Level 2 heralds the first emergence of some important domain-specific ideas (science as concerned with explanatory mechanism; experiments as a means for hypothesis testing) and represents one set of ideas that are transitional between these two epistemologies. On the one hand, a concern with explanation and testing does not immediately undermine one's belief in the true and certain nature of knowledge (e.g., one can believe that explanations are simple inductions from data, and that experiments can definitely prove one's hypothesis to be true). On the other, an acknowledgment that scientists are concerned with explanation and testing can sow seeds for appreciating the constructed, tentative nature of knowledge, especially as students begin to realize the conjectural nature of scientific explanations.
C. Excerpt that describes key features of elementary science curricula that support epistemological development (i.e., movement toward more constructivist epistemologies) (pp. 402-409).
Implications for the Teaching of Elementary School Science
Our work demonstrates that school science experiences can dramatically affect the development of epistemological thinking about science during the elementary school years. More specifically, the sixth-grade students in the constructivist classroom had clearly developed a more constructivist epistemology of science than students in the comparison classroom (or, for that matter, the students in previous studies). We would argue that the main factor responsible for the two groups' different epistemological stances towards science was the difference in their elementary school science experiences. Both groups were the same age (to control for maturationally based developmental factors) and demographically quite similar (to control for the influence of parents and outside of school experiences with science). Furthermore, other school subjects (for students in the constructivist science classroom) were taught from more traditional epistemological perspectives, making it unlikely that the students developed their constructivist insights from these other elementary school experiences. Both groups even had similar amounts of elementary classroom time spent on science. The main difference between the two groups was the target epistemology of science that the teachers (implicitly or explicitly) aimed to help their students develop and applied when designing their science curricula.
Other researchers (e.g., Brown & Campione, 1994; Lehrer et al., in press; Metz, in press; White, 1993) have already demonstrated that elementary school children are more "ready" to engage with issues of theory building and data gathering than has been assumed by those operating from a Piagetian-based developmental constraints perspective. What the present research adds is evidence that they also are able to build more sophisticated epistemological understandings about science than has been assumed or demonstrated in the prior literature. We attribute these developments to the innovative educational environments which provide intensive teacher scaffolding and support for student inquiry. Taken together, both kinds of research not only challenge the prior conventional wisdom about the kinds of intellectual demands a developmentally appropriate elementary science curriculum can and should make, but also begin to provide valuable alternative models of what truly empowering and effective elementary school science curriculum can and should be like.
Design Features of an Elementary Science Curriculum that Appear to Support the Development of a Constructivist Epistemology
But what was it about Hennessey, her teaching, and her "constructivist" classroom environment that contributed to the tremendous growth in her students' epistemological views? We believe that many coordinated aspects of her teaching approach were essential. Although our study was not designed to address this issue directly, we conclude by discussing what some of these coordinated features may have been and the ways they may have supported epistemological development. Our discussion is informed by what we know about Hennessey's classroom from the work of those who have studied her classroom directly (Beeth, 1998; Beeth & Hewson, 1999a, 1999b,Hennessey, 1994b, in press; Hennessey & Beeth, 1993) and from our own informal observations. They also are informed by prior research and theoretical writings on features of classroom environments that may be particularly important in promoting epistemological understanding and conceptual change 8.
Authentic inquiry. First, Hennessey gives her students responsibility for managing most aspects of their own inquiry. Although she generally begins units by giving students a set of phenomena to explore, it is then the students' task to record the questions they have about these phenomena, to select questions they want to pursue further, and to plan ways to pursue their investigations. In these respects, Hennessey routinely involves her students in what Roth & Roychoudhury (1993) have called authentic contexts for scientific inquiry: contexts in which students have responsibility for posing questions, generating methods and analyzing data. This form of more "open" inquiry starkly contrasts with the more "closed" laboratory exercises used in traditional science classrooms, in which the problems, methods, and often even expected answers are given to students ahead of time. Some advantages of more authentic inquiry are that it ensures that the questions investigated make sense to the students (as they are grounded in what they know and think) and it elevates student motivation, interest, and involvement. In addition, as Chinn and Malhotra (in press) point out, there is an even deeper reason that involving students in more authentic inquiry may be particularly important in promoting epistemological development. By leaving open both the question of problem and method, students must confront a number of thorny issues about the interplay between theory and evidence that never get raised in more standard exercises. These authors analyze the detailed ways in which more authentic experimentation and inquiry supports the development of a more constructivist epistemology and traditional laboratory exercises support a more inductivist or positivist view. Significantly, many of the innovative curriculum units developed for elementary school students in the last decade have all involved students in authentic inquiry (Brown & Campione, 1994; Lehrer et al., in press; Metz, in press; Roth, 1996; White, 1993).
Generative problems. Second, Hennessey selects initial problems that invite her students to consider issues of deep disciplinary significance. Gardner, Perkins, Wiske, and colleagues call these "generative topics" (Gardner, 1999; Wiske, 1997): topics that open up rich veins of inquiry within a discipline, such as science, mathematics, history, or the arts. For example, in one curricular unit, Hennessey's students explore their ideas about the day/night cycle and the causes of the seasons in ways that encourage them both to think about the relations between the earth, sun, and other elements of the solar system, and to build models of these relations. In another unit, students explore the motions of everyday objects and work with each other to develop ways of describing these motions. They wrestle with the difficult problem of how to describe the motions in a clear and consistent manner and ultimately raise deeper questions (explored in a later grade and unit) about how to explain these motions. In other units, students explore phenomena that involve them in theorizing about nature of heat, matter, gravity, living things, heredity, and the origins of the universe.
These topics all involve areas where students' starting conceptions can be quite fuzzy and different from the ideas of science experts. Thus, in pursuing their investigations, students must work to clarify and understand their own initial ideas. They also encounter both anomalies that challenge their thinking, and new ideas (from their teacher and others) that contribute to the process of conceptual change.
Most of the reform curricula showcased in the literature also stress the importance of picking problems that reveal important principles. However, these curricula vary in whether they focus on important design and engineering principles (Roth, 1996), on important methodologies for investigating a domain (Metz, in press), or on underlying domain-specific theories that involve students in conceptual changes (Brown & Campione, 1994; Hennessey, in press; White, 1993). We believe that Hennessey's deliberate choice of problems which are on the frontiers of student understanding provides her students with a particularly rich opportunity to learn that ideas are multi-faceted and involve explanatory conjectures that go beyond the information given. These problems also allow students to experience the difficulties in coming to understand their ideas and to learn about the kinds of mental work that go into understanding and clarifying ideas.
Representing ideas in multiple ways. A third feature of Hennessey's approach is her emphasis on having students take responsibility for representing their ideas in multiple ways. Clearly, if the focus of the curriculum is on the development and elaboration of student ideas, it is important to find ways to make those ideas public and open to inspection and debate. Not only do explicit representations help students concretize and systematize inherently abstract and complex ideas, they also help students clarify ideas or discover aspects of their ideas that are not clear to them. Finally, as has been well documented in the conceptual change literature, making ideas public facilitates the process of conceptual change itself (e.g., Hewson & Hewson, 1983; Minstrell, 1982; Smith et al., 1997).
Hennessey encourages students to use a variety of means to make their ideas public, including poster production, concept maps, physical models, drawings of conceptual models, word processing to write out ideas, audio-tapes to dictate ideas, and small and whole group discussion to present ideas orally. Poster production, audio recordings, and written statements not only serve to make ideas public, but also preserve a record of those ideas so that students can explicitly compare earlier and later ideas. Significantly, Hennessey encourages her elementary school students to represent, share, and analyze their ideas about domain-specific science concepts as well as their metaconceptual ideas about thinking, learning, and science. For example, students were asked to create concept maps of their notion of ideas and of the terms intelligible, plausible, fruitful, and to write word-processed essays in which they expressed their beliefs about the nature of learning and science.
Collegial learning communities and metacognitive discourse. The fourth and fifth features of Hennessey's teaching approach that we believe are central to enhancing the development of a constructivist epistemology among her students are the kinds of social and discourse structures that characterize her classroom. She has created what Brown & Campione (1994) call a community of learners, where social dialogue and collaboration is an essential aspect of the learning process, yet where each student's voice is heard, respected, and valued. Students work together in a variety of ways—planning and conducting investigations; negotiating the meaning of words; learning to listen, share, and raise questions about each other's views—much in the way a community of scientists works together in developing and considering the viability of each other's ideas.
In such an environment, the teacher's role is complex: Often she serves as a facilitator and scaffolder of student inquiry. At other times, she introduces the views of members of the professional "science community" for her students to consider. This kind of social environment facilitates students' awareness of the diversity of viewpoints and the ways in which they may (or may not) fully understand the ideas of self and others. It also widens the range of ideas students consider, which often leads them to develop more complex views. Given this kind of social environment, it is not surprising that students view these social interactions as vitally important to the learning and knowledge acquisition processes.
The collegial social environment in Hennessey's classroom calls for and is supported by an explicit "metacognitive" discourse among students about their ideas. In her own research, Hennessey (in press) has extensively described the nature of this discourse and the variety of ways that the elementary students in her classroom are encouraged to develop metacognitive abilities. These include explicitly stating or identifying their own conceptions, considering the reasoning used to support a conception, considering the implications of a conception, temporarily bracketing or setting aside one's own conceptions in order to consider the competing views of others, reflecting on the status of conceptions of self and others (i.e., their intelligibility, plausibility, and fruitfulness), and evaluating the consistency and generalizability of a set of conceptions. She does not, of course, expect students to have all these metaconceptual skills initially. Rather, it is an explicit goal of her curriculum to help students build increasingly sophisticated metaconceptual skills and understandings over a 6-year period. (See Table 1 for a description of metaconceptual goals for students at each grade level and the way she ups the ante for students in grades 4-6).
In a recent observational study, Beeth and Hewson (1999a) described the complex kind of discourse that occurred in Hennessey's sixth-grade classroom during a 37-day unit on force and motion. They believed a crucial part of the artistry of her pedagogy is the way she and her students weave among three kinds of discourse throughout the unit: discourse about specific science concepts, metacognitive discourse concerning the status of their ideas, and discourse about epistemological standards. They also believed the depth of understanding her students achieve is significantly influenced by three sources of authority at play in this learning community: curricular authority, authority of epistemological standards, and personal authority. Curricular authority is in the hands of the teacher as she chooses concepts for study and the depth of target understandings. The authority of the scientific community's epistemological standards is introduced by the teacher when students are ready to apply them, by teacher-initiated questions such as: Do you have evidence for your ideas? Are your ideas consistent with other ideas? Can you use your ideas to make predictions about new situations? Students also negotiate and apply their own epistemological standards. This personal authority is exercised by the students as they determine what to understand and ways to apply their ideas to new contexts. Hennessey respects and nurtures this personal authority by providing ample time for students to work with ideas, to negotiate standards for judging ideas, and to explore the status of ideas.
We believe that the discourse in Hennessey's classroom has all the elements of what van Zee and Minstrell (1997) called reflective discourse, a kind of discourse that they argued is crucial to supporting the process of conceptual change. In contrast to the teacher- controlled discourse of more traditional classrooms which follows the rapid-fire IRE format (teacher initiates question, student responds, teacher evaluates correctness of student response and then moves on to the next question and student), reflective discourse is more student-centered, slower paced, and open ended. In particular, the questions and comments raised by the teacher or other students occur in reaction to student initiated comments and often have the structure of a reflective toss (student utterance, teacher or student question or comment, student utterance). Such questions and comments may probe for clarification and elaboration of meanings, draw out a variety of views in a neutral manner, and encourage students to monitor the discussion and their own thinking. Both students and teacher take the important roles of questioners and commentators, and vigorous student-student-student reflective dialogues ensue.
Although reflective discourse with these features has been described for a variety of reform curricula both at the elementary and high school levels (Brown & Campione, 1994; Hennessey, in press; Lampert, 1990; Lehrer et al., in press; Metz, in press; Minstrell, 1982), there may be distinctive differences in the ways this type of discourse is orchestrated and the relative importance placed on its different components. For example, some teachers seem to focus on scaffolding discourse about evaluating an idea in relation to its fit with evidence (Brown & Campione, 1994; Lehrer et al., in press;Metz, in press). Other teachers, such as Hennessey (in press), seem to put greater emphasis on scaffolding discourse about evaluating an idea in light of a variety of criteria: its intelligibility, its fit with their prior ideas, and its fit with evidence. The way these differences manifest in a given reflective discourse not only interacts with how the acts of inquiry occur in the classroom, but also may have implications for the epistemological lessons students learn from the curriculum in which the discourse evolves. Perhaps one reason that the students in Hennessey's classroom were so aware of the guiding role ideas play in scientific inquiry was the great emphasis she placed on having them evaluate their ideas not only in terms of fit with evidence, but also in terms of intelligibility and fit with their prior ideas.
Other features. A variety of additional factors may have contributed to the effectiveness of Hennessey's curriculum in bringing about change in student epistemological understandings. Hennessey is a knowledgeable scientist, with graduate study in the biological sciences. Her depth of scientific knowledge, as well as her willingness to research topics or contact experts, allows her to respond flexibly and intelligently to the questions and issues her students raise. She is knowledgeable of research on student conceptual frameworks and of reform efforts to teach science from a constructivist perspective, having completed doctoral work in science education. She, herself, has sophisticated epistemological views toward science. In addition, she is highly experienced at teaching elementary science from a constructivist perspective, having worked from this perspective with students over the last 20 years. Finally, by teaching science in a school which allows her to work with the same students over a 6-year period (and by having a student body that is relatively stable), she has an extended time scale which makes it more likely that deep conceptual change can occur. She has unique opportunities to get to know her students and their thinking, to invite them to revisit and deepen their understanding of topics at varying points throughout the curriculum, and to remind them of their earlier views (e.g., she pulls out posters saved from prior years and discusses with students how their ideas have changed). In all of these respects, her classroom may represent a best case scenario for bringing about change in students' epistemological understandings.
However, we believe that we can learn a great deal from careful analysis of best case scenarios. They inform us of what is educationally possible given the prior concepts and developmental limits of elementary schoolchildren. What we learn is that elementary school children are much more capable of engaging with theory building and epistemological issues than many have assumed. Best case scenarios also can contribute to our understanding of exemplary educational practice and to our developing a more adequate vision of what the central goals of an elementary science curriculum can and should be. Like a number of other researchers in the field, we believe it may be particularly important to develop students' epistemological understandings early, as these views can provide an exciting and empowering framework to build upon in their subsequent science educational experiences.
References
Beeth, M.E. (1998). Teaching science in 5th grade: Instructional goals that support conceptual change. Journal of Research in Science Teaching, 35 (10), 1091-1101.
Beeth, M.E. & Hewson, P.W. (1999a, March). Facilitating learning of science content and scientific epistemology: Key elements in teaching for conceptual change. Paper presented at the National Association for Research in Science Teaching, Boston.
Beeth, M.E. & Hewson, P.W. (1999b). Learning goals in an exemplary science teacher's practice: Cognitive and social factors in teaching for conceptual change. Science Education, 83, 738-760.
Brooks, J. G., & Brooks, M.G. (1993). In search of understanding: The case for constructivist classrooms. Alexandria, VA: Association for Supervision and Curriculum Development.
Brown, A.L. & Campione, J.C. (1994). Guided discovery in a community of learners. In K. McGilly (Ed.), Classroom Lessons: Integrating Cognitive Theory and Educational Practice (pp.229-270). Cambridge, MA: MIT/Bradford Press.
Carey, S. (1991) The Nature of Science Interview. Unpublished manuscript.
Carey, S., Evans, R., Honda, M., Jay, E., & Unger, C. (1989). "An experiment is when you try it and see if it works": A study of grade 7 students' understanding of the construction of scientific knowledge. International Journal of Science Education, 11, 514-529.
Carey, S. and Smith, C. (1993). On understanding the nature of scientific knowledge. Educational Psychologist, 28, 235-251.
Chinn, C.A. and Malhotra, B.A. (in press). Epistemologically authentic scientific reasoning. In K. Crowley, C.D. Schunn, & T. Okada (Eds), Designing for science: Implications from professional, instructional, and everyday science. Mahwah, NJ: Erlbaum.
Clement, J. (1989). Learning via model construction and criticism: Protocol evidence on sources of creativity in science. In J. Glover, R. Ronning, & C. Reynolds (Eds.), Handbook of creativity: Assessment, theory and research (pp. 341-381). New York: Plenum.
Clement, J. (in press). Model construction in scientists and students: Case studies of imagery, analogy, and physical intuition. Mahwah, NJ:Lawrence Erlbaum Associates, Inc.
Gardner, H. (1999). The disciplined mind. NY: Simon & Schuster.
Haber-Schaim, U., Abegg, G., Dodge, J., Kirksey, H., & Walter, J. (1987). Introductory physical science. Englewood Cliffs, NJ: Prentice Hall.
Hennessey, M. Gertrude. (1994a, May). Conceptual change approach to learning science: The dynamic role of metacognition. Paper presented at the Annual Meeting of the National Association for Research in Science Teaching, Anaheim, CA.
Hennessey, M. G. (in press). Probing the dimensions of metacognition: Implications for conceptual change teaching-learning. In G.M. Sinatra & P.R. Pintrich (Eds.), Intentional conceptual change. Mahway, NJ: Lawrence Erlbaum Associates.
Hennessey, M.G. and Beeth, M. (1993, April). Students' reflective thoughts about science content: A relationship to conceptual change learning. Paper presented at the American Educational Research Association meeting, Atlanta, Georgia.
Hewson, M. and Hewson, P. (1983). Effect of instruction using students' prior knowledge and conceptual change strategies on science learning. Journal of Research in Science Teaching, 20, 731-743.
Lampert, M. (1990). Connecting inventions with conventions. In L. Steffe and T. Wood, (Eds.). Transforming children's mathematics education (pp.253-265). Hillsdale, NJ: Erlbaum
Lederman, N. (1992). Students' and teachers' conceptions of the nature of science: A review of the research. Journal of Research in Science Teaching, 29, 331-359.
Lehrer, R., Carpenter, P., Schauble, L., and Putz, A. (in press). Designing classrooms that support inquiry. In: J. Minstrell and E. van Zee (Eds.) Teaching in the inquiry-based science classroom. Washington, D.C.: American Association for the Advancement of Science.
Metz, K. (in press). Young children's inquiry in biology: Building the knowledge-bases to empower independent inquiry. In: J. Minstrell and E. van Zee (Eds.) Teaching in the inquiry-based science classroom. Washington, D.C.: American Association for the Advancement of Science.
Minstrell, J. (1982). Explaining the 'at rest' condition of the object. Physics Teacher, 20, 10-14.
Nercessian, N. (1993). How do scientists think? Capturing the dynamic of conceptual change in science. In R. N. Giere (Ed.), Minnesota studies in the philosophy of science: Vol. 15. Cognitive models of science (pp.3-44). Minneapolis: University of Minnesota Press.
Perkins, D., Schwartz, J., West, M., & Wiske, M. (1995). Software goes to school. Oxford, England: Oxford University Press.
Posner, G., Strike, K., Hewson, P., & Gertzog, W. (1982). Accomodation of a scientific conception: Toward a theory of conceptual change. Science Education, 66, 211-227.
Roth, W. M. (1996). Teacher questioning in an open-inquiry learning environment: Interactions of context, content and student responses. Journal of Research in Science Teaching, 33, 709-736.
Roth, W. and Roychoudhury, A. (1993). The development of science process skills in authentic contexts. Journal of Research in Science Teaching, 30, 127-152.
Smith, C., Maclin, D., Grosslight, L., & Davis, H. (1997). Teaching for understanding: A study of students' preinstruction theories of matter and a comparison of the effectiveness of two approaches to teaching about matter and density. Cognition and Instruction, 15, 317-394.
Snir, J., Smith, C., & Grosslight, L. (1993). Conceptually enhanced simulations: A computer tool for science teaching. Journal of Science Education and Technology, 11, 373-388.
Van Zee, E. & Minstrell, J. (1997). Using questioning to guide student thinking. The Journal of The Learning Sciences, 6, 227-269.
White, B. (1993). ThinkerTools: Causal models, conceptual change, and science education. Cognition and Instruction, 10 (1), 1-100.
White, R. & Gunstone, R. (1989). Metalearning and conceptual change. International Journal of Science Education, 11, 577-586.
Wiske, M.S. (1997). Teaching for understanding. San Francisco: Jossey-Bass, Publishers.
8 See Lederman (1992) for a review of classroom environment features (at the high school and college level) that are associated with growth in student understanding of the nature of science. The findings from those studies are consistent with the arguments made here about critical features of an elementary school science classroom.
Smith, C., Maclin, D., Grosslight, L., & Davis, H. (1997) Teaching for Understanding: A Study of Students' Preinstruction Theories of Matter and a Comparison of the Effectiveness of Two Approaches to Teaching about Matter and Density". Cognition and Instruction, 15 (3), 317-393.
Smith, C., Maclin, D., Houghton, C. and Hennessey, M. (2000) Sixth-Grade Students' Epistemologies of Science: The Impact of School Science Experiences on Epistemological Development. Cognition and Instruction, 18 (3), 349-422.